Finding the slope that divides an area in half.

The picture is

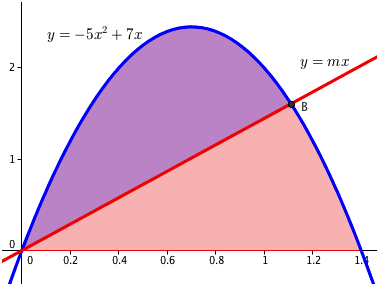
The total area under the parabola is found by evaluating $\int_0^{7/5} 7x - 5x^2\;dx$. This gives a value of 343/150. For a line of slope $m$ through the origin with equation $y = mx$, we want to calculate $\int_0^{x_B} (7x - 5x^2) - mx\;dx$, where $x_B$ is the x-coordinate of point B, the intersection point of the line and the parabola. This integral gives the area of the purple colored region in the picture. We then set the value of this integral equal to 343/300 (one half of the area of the parabolic region, and solve for $m$.

The first thing to do is to find an expression for $x_B$ in terms of the slope $m$. We do this by solving the system of the equations corresponding to the two graphs

$$\begin{align*} y &= mx\\ y &= 7x - 5x^2 \end{align*}$$

Setting the equations equal to one another and solving for $x$ gives $x = 0 \text{ or } x = \frac{7 - m}{5}$. The non-zero value is our $x_B$. Therefore, the integral we need to evaluate is

$$ \int_0^{(7-m)/5} 7x - 5x^2 - mx\;dx $$

Using FTC 2 and evaluating between the limits of integration gives the expression

$$ \frac{7}{2}\left(\frac{7-m}{5}\right)^2 - \frac{5}{3}\left(\frac{7-m}{5}\right)^3 - \frac{1}{2}m\left(\frac{7-m}{5}\right)^2$$

Lets factor out $\left(\frac{7-m}{5}\right)^2$ and set the expression equal to 343/300.

$$\left(\frac{7-m}{5}\right)^2 \left[\frac{7}{2} - \frac{5}{3}\left(\frac{7-m}{5}\right) - \frac{m}{2}\right] = \frac{343}{300} $$

Now combine the fractions in the brackets and simplify to get

$$\left(\frac{7-m}{5}\right)^2\left[\frac{7-m}{6}\right] = \frac{343}{300}$$

Multiplying out the left hand side, then multiplying through by 150 gives

$$(7 - m)^3 = \frac{343}{2}$$

Finally, taking cube roots and solving for $m$ gives

$$ m = 7 - \sqrt[3]{\frac{343}{2}} = 7 - \frac{\sqrt[3]{343}}{\sqrt[3]{2}} = 7 - \frac{7}{\sqrt[3]{2}} = 7 - \frac{7\sqrt[3]{4}}{2} \approx 1.4441$$

TADA!!